True ML Talks #20 - Transformers, Embeddings and LLMs - ML Scientist @ Turnitin

We are back with another episode of True ML Talks. In this, we'll delve deep into the main ideas of the fascinating paper titled Analyzing Transformer Dynamics as Movement through Embedding Space. This paper introduces a novel perspective on how Transformers operate, emphasizing that they learn an embedding space and navigate it during the inference process. We are talking with Sumeet Singh
Sumeet is a Distinguished ML Scientist at Turnitin, and the author of the paper we are going to be discussing today. He also comes from a research background.
- Understanding Transformer Dynamics
- Demystifying Embedding Space in Transformer Models
- Deciphering the Mechanics of Token Prediction in Transformers
- Unique Abstractions of Transformer Layers
- The Mystery of Repetitive Tokens
- The Misleading Notion of Learning in Transformer Models
- The Interplay of In-Context Learning, Few-Shot Learning, and Fine Tuning in Transformers
- Navigating General-Purpose AI: Model Choices and Practical Insights
Watch the full episode below:
Understanding Transformer Dynamics: A Deep Dive into Embedding Space
In the realm of AI and natural language processing, the Transformer model reigns supreme for text processing and generation. But what lies beneath this impressive architecture? The groundbreaking paper, "Analyzing Transformer Dynamics as Movement to Embedding Space," unravels the mysteries of the Transformer's inner workings.

This research began when developing an auto-grading model for short answers, achieving an impressive 80% accuracy rate across subjects but lacking clarity on its mechanisms. To understand the Transformer's behavior, the study delved deep, initially exploring attention attribution and weight analysis with limited insights, leaving researchers puzzled.
1. A Paradigm Shift: Viewing Transformers in Embedding Space
The turning point in this research came with the realization that the Transformer could be viewed as a series of operators in an embedding space. This space, like a three-dimensional landscape, guides the Transformer's predictions. Instead of seeking attention patterns, the perspective shifted to viewing the Transformer as a river flowing through valleys and canyons, following paths of least entropy.
2. The Fixed Embedding Space
Once the model is trained, the embedding space remains fixed. When presented with the same input sequence, it consistently produces identical embeddings. These embeddings are crucial in predicting the next token, as they determine the probabilities assigned to each token in the sequence.
3. Angular Proximity and Token Prediction
The research uncovered that the embedding space organized itself into a bounded space resembling a ball, thanks to layer normalization. The model's token predictions heavily rely on the angular proximity between the aggregated embedding vector and individual token embeddings.
4. Decoding Walk vs. Encoding Walk
Two distinct walks shape the Transformer's behavior: the decoding walk, which governs stochastic decoding and token sampling, and the encoding walk, a deterministic process that forms soft clusters based on the similarity of token vectors. The encoding walk is a key factor in transforming a sequence of token vectors into a single aggregated embedding vector.
5. Level of Abstraction in Transformers
Unlike conventional neural networks where lower layers work at lower levels of abstraction, Transformers maintain a consistent level of abstraction throughout their layers. This is evident in the shared input and output embedding matrices, highlighting the unique nature of Transformer architecture.
Demystifying Embedding Space in Transformer Models
To grasp the concept of embedding space, we must first recognize it as the vector space of size d_model—the hidden size of the Transformer. In simpler terms, d_model represents the dimensionality of this space. For instance, in GPT models, this dimension can be substantial, reaching up to 12,000.
Now, what's vital to comprehend is that every vector emerging from every layer of the Transformer model resides within this embedding space. This includes not only the input token vectors but also all the vectors generated as you move up the layers, all the way to the top—culminating in the context vector.
It's essential to clarify that the size of the embedding space isn't determined by the number of parameters in the model or the top layer's representation. Instead, it's exclusively defined by the value of d_model. This key distinction ensures that we have a clear understanding of what constitutes the embedding space in Transformer models.
Deciphering the Mechanics of Token Prediction in Transformers
In our quest to comprehend the inner workings of Transformers, we now arrive at a pivotal juncture: the mechanics of token prediction. Sumeet, with his insightful perspective, sheds light on the intricate processes that dictate how Transformers generate sequences of text and make intelligent predictions.
1. The Role of Language Modeling Head:
At its core, this language modeling head is a matrix—a matrix with dimensions d_model by V, where V represents the size of your embeddings, which can be substantial depending on your tokenization scheme. This matrix plays a pivotal role in mapping context vectors to token probabilities.
2. The Magic of Dot Products:
The essence of token prediction lies in the dot product—a similarity metric that governs the Transformer's decision-making. When the context vector, derived from the final layer of the decoder, undergoes matrix multiplication with the language modeling head, it results in a vector of probabilities. This probability distribution determines the likelihood of each token in the sequence.
3. Mapping Sequences into the Neighborhood
Now, let's consider the profound concept of mapping a sequence into the neighborhood of a token. The objective is to transform a sequence of tokens, from W_1 to W_t, into the vicinity of W_t+1. This process is akin to navigating a path that appears intelligent to human observers.
4. The Intelligent Machine
At the heart of this transformation is the creation of an intelligent machine—a machine that takes a sequence and skillfully maps it to the neighborhood of the next token. The intelligence lies in the subtlety and coherence of the path, as each step in the walk is evaluated for its degree of intelligence.
5. The Role of Position Encodings
Unlike Convolutional Neural Networks (CNNs), Transformers do not employ pattern recognition kernels. However, there exists a fascinating element known as relative position encodings within the attention layers. These static encodings influence the aggregation weights and help counter self-bias.
6. Negative Self-Bias
Understanding self-bias is crucial. Without position encodings, a context vector would be inclined to attract vectors similar to itself, resulting in repetitive predictions. Position encodings introduce negative self-bias, suppressing the context vector's affinity for itself and promoting diversity in predictions.
7. Position Kernels
Delving deeper, we discover that position kernels, as revealed in the paper, serve to shape the self-bias disposition. They skew aggregation weights, influencing which positions are favored and which are not.
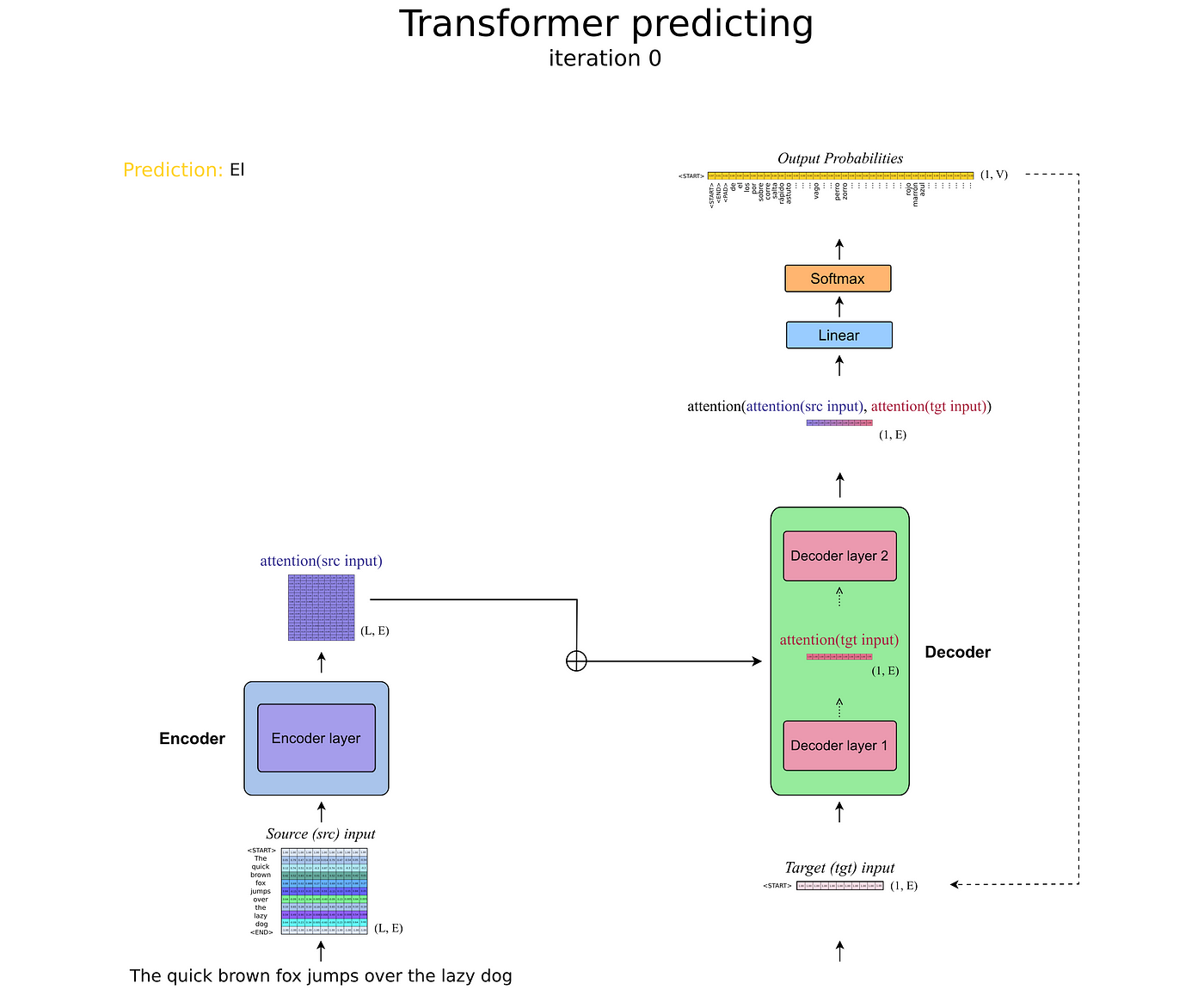
Here is a really great blog that explains Transformer Architecture one step at a time:

Unique Abstractions of Transformer Layers
As we delve deeper into the fascinating world of Transformer models, a compelling insight is brought forth—one that distinguishes Transformers from conventional neural networks like CNNs. The question at hand is, why do Transformers operate differently, and how can we grasp the concept of layer-by-layer embeddings?
Distinction Between Transformers and CNNs:
- Transformers operate differently from CNNs. In CNNs, lower layers typically capture simpler features like edges, while higher layers build more complex representations.
- In contrast, Transformers work within the same abstract space across all layers, without a clear hierarchy of abstraction like in CNNs.
Understanding the Residual Stream:
- Transformers maintain uniformity in their abstract space partly due to the presence of a residual stream.
- In a Transformer layer (e.g., in the encoder), there is an input followed by an attention layer. A residual link adds the output of the attention layer back to the input.
- Similarly, in the feed-forward layer, transformations are applied, and another shortcut adds the output back to the input.
- This consistent addition of input and output at each layer ensures that dimensions maintain the same meaning, creating a unified abstract space.
The Layer-by-Layer Mental Model:
- To help understand this phenomenon, the concept of "layer-by-layer embeddings" is introduced.
- In CNNs, there's a hierarchical construction of abstraction layers. However, in Transformers, each layer contributes to the same abstract space.
- Transformers challenge the traditional understanding of neural network behavior by presenting a network of layers that work together in a more unified manner.
The Mystery of Repetitive Tokens: Small vs. Large Transformer Modelsa
In the world of Transformers, an intriguing observation is the tendency of smaller models to repeat tokens, while larger models produce more varied output. Sumeet explores this phenomenon, though it lacks a clear theoretical explanation.
- Smaller Models: Smaller Transformers often exhibit token repetition in generated text, highlighting an intriguing link between model size and output quality.
- Richer Embedding Space: A key factor contributing to the difference between small and large models is the richness of the embedding space. Larger models have a more extensive, nuanced feature space for intricate information processing.
- More Parameters for Granular Processing: Larger models have more layers and parameters, especially in feedforward layers. This enhances their ability to process information in a sophisticated manner.
- Decoding Strategies: Token repetition can be mitigated by choosing the right decoding strategy. Greedy Decoding and Beam Search are more prone to repetition, whereas techniques like Top-K or Top-P sampling yield diverse results.
- Repeated Sentences: Even in larger models, occasional sentence repetition occurs, revealing the complexity of text generation within Transformers.
The Misleading Notion of Learning in Transformer Models
In the realm of Transformer models, a crucial question arises: Does genuine in-context learning take place in these models, or is it more aptly described as a cleverly framed concept? The research paper challenges conventional notions of learning within Transformers and unveils the underlying mechanisms.
Traditional learning involves adjusting weights and parameters to facilitate a model's adaptation and response to new data. However, this conventional understanding doesn't align with Transformer models. The core issue lies in their fixed embedding space and predefined paths.
In essence, these models do not engage in learning in the traditional sense. The embedding space remains static, and the paths, though diverse, are predetermined. During inference, there is no adaptation or modification of model weights. Instead, these models navigate a landscape of possibilities, with each missing element serving as a unique starting point.
The research also addresses the ongoing debate regarding these models' intelligence and reasoning abilities. Some argue that they lack the mechanisms for genuine reasoning, relying instead on predictions based on memorized data rather than true comprehension.
Furthermore, the paper delve into the denoising process, a fundamental operation shared by these models. When tokens are randomly blanked, the context web remains intact, regardless of the blank token's position. The model adeptly consolidates this dual-context into a single context vector, ensuring seamless operation, regardless of the missing elements' location.
There is no learning happening. I mean, because embedding space is fixed. All the paths are fixed. All you’re doing is picking, choosing. So what learning here? Your weights are not changing. Nothing! - Sumeet Singh
The Interplay of In-Context Learning, Few-Shot Learning, and Fine Tuning in Transformers
In the paradigm described, where Transformers navigate predetermined paths within a fixed embedding space, the relationships between "In-Context Learning," "Few-Shot Learning," and "Fine Tuning" acquire distinct perspectives.
1. In-Context Learning and Few-Shot Learning
Within this paradigm, In-Context Learning and Few-Shot Learning converge into a shared concept. Whether it's a conversation history or a set of examples, they both boil down to contextual sequences. When a Transformer model encounters a novel context, it selects a path through the embedding space based on that context. This path selection process, dictated by the context, defines the model's output. Hence, both In-Context Learning and Few-Shot Learning involve the model adapting to a provided context and generating contextually relevant responses or outputs.
2. Fine Tuning as Path Modification
Supervised Fine Tuning, in the Transformer context, represents a process of altering the predefined paths within the embedding space. During fine-tuning, additional data and specific objectives are introduced, reshaping the internal geography of the model. While the fundamental mechanism—path selection—remains consistent, the landscape of available paths undergoes adjustments to align with the desired fine-tuning task.
3. RLHF and Signal Propagation
In the case of Reinforcement Learning from Human Feedback (RLHF), the key divergence lies in how the reinforcement signal propagates. While supervised fine-tuning employs token-level cross-entropy loss, RLHF harnesses signals from an evaluation model. What sets RLHF apart is that the reinforcement signal extends across the entire sequence, influencing the model's paths comprehensively. However, both RLHF and supervised fine-tuning share the common objective of reshaping the map of undulations within the embedding space to optimize performance for specific tasks.
Transformer models have a remarkable adaptability across modalities. These models seamlessly transition from text to images, speech, and diverse datasets.
Traditionally, sequences have a linear flow of context, but when shifting to images, the concept of a linear sequence becomes intriguing. Models like Bard handle this by using denoising. Blank tokens, regardless of their position, retain context. Whether at the start, middle, or end, a context web forms, and the model aggregates it into a single context vector, adapting seamlessly.
Navigating General-Purpose AI: Model Choices and Practical Insights
- Shift to General-Purpose AI: Treat Transformers as versatile intelligence machines, simplifying model complexities.
- Model Variations Matter Less: Deep understanding reduces model distinctions, emphasizing real-world performance.
- Practical Model Selection: Choose models based on real-world task evaluation, prioritizing efficiency.
- Leveraging Prompt Engineering: Tailor inputs for effective guidance without model intricacies.
- Cost-Efficient Fine-Tuning: Smaller models for cost-effective high-traffic performance.
- Balancing Cost & Performance: Crucial factors for efficiently serving fine-tuned models in high-traffic scenarios.
Read our previous blogs in the True ML Talks series:

Keep watching the TrueML youtube series and reading the TrueML blog series.
TrueFoundry is a ML Deployment PaaS over Kubernetes to speed up developer workflows while allowing them full flexibility in testing and deploying models while ensuring full security and control for the Infra team. Through our platform, we enable Machine learning Teams to deploy and monitor models in 15 minutes with 100% reliability, scalability, and the ability to roll back in seconds - allowing them to save cost and release Models to production faster, enabling real business value realisation.


